The Man Who Knew Infinity

( This post was published at History Under Your Feet, reproducing the same).

Way back in the 1914 Prof G.H.Hardy, a famous British mathematician, went to see his friend, who was recovering from an illness in a hospital, in London’s Putney district. He remarked to him, that he had come in a cab which had a number 1729, and some how that number seemed, dull and unremarkable to him. To which his friend immediately replied

“No Hardy, it’s a very interesting number, it is the smallest number that can be expressed as the sum of two cubes in two different ways”.

To the mathematically challenged, it means that 1729 can be expressed as

1729 = 1728+1 = 12^3 + 1^3
1729 = 1000+729 = 10^3 + 9^3

This was an anecdote, which we often read as school students, and even during our mathematics classes. The friend here is of course Srinivasa Ramanujan, one of India’s greatest scientists and one of the world’s greatest mathematicians.

The bonding between Hardy and Ramanujan was much earlier though. Exactly a year back, Hardy received a letter from Ramanujan,  then working as a clerk at Madras Port Trust.  It was a 10 page letter, which had around 120 statements on theorems, continued fractions and number theory.  Initially Hardy dismissed that letter as a crank, the ones mathematicians usually get, but a second look made him revise his opinion. He discussed it over with his colleague, J.E.Littlewood, and their conclusions “the results must be true because, if they were not true, no one would have had the imagination to invent them”.

The world of mathematics owes a great debt to India , because this is the land from which the basic theories of mathematics have originated. Aryabhatta who contributed the number-place value system and the concept of zero, as well as calculating the area of the triangle. Bhaskara who came up the concept of the decimal system. Halayudha who provided a clear description of the Pascal’s triangle.  And between 1300-1600 AD, we had the Kerala school of Mathematics and Astronomy founded by Madhava of Sangamagrama which made significant contributions to the fields of  infinite series and calculus.

Ramanujan was born into an Iyengar family, in the town of Erode, Tamil Nadu on Dec 22, 1887. His father was a clerk in a saree shop, while his mother was a devout Brahmin housewife. Theirs was a typical Tamil Brahmin household, pretty religious and orthodox. Growing up under his mother’s care and guidance, he learnt about Indian tradition and puranas. His first brush with mathematics was in 1898, in Higher Secondary School.  And that was when his prodigal talent came to being. At 11 years, he exhausted the mathematical knowledge of two college students. Again in school, Ramanujan was absolutely brilliant at maths, but quite often flunked in the other subjects. Consider this by the time he was 13, he mastered SL Loney’s work on Advanced Trignometry, soon he developed his own methods to solve the quartic function.

The book that influenced Ramanujan the most though was Synopsis of Pure Mathematics by G.K.Carr that had around 5000 theorems, when he was 16. .The book a collection of around 5000 theorems,  stoked his curiosity, made him explore mathematics much more deeper.  The following year, Ramanujan, developed and investigated the Bernoulli numbers, calculated the Euler-Mascheroni constant up to 15 decimal places, winning him a new found respect among his peers.

His genius though would be a sort of curse for him, fact is Ramanujan was interested only in maths, he hardly cared about other subjects at school and college. So while he passed Maths with distinction, he was below par in the other subjects. And this meant that Ramanujan failed his Fellow of Arts exam in 1906, in spite of his brilliance at Maths, and with no formal degree, he had to pursue maths research on his own, at times living in dire poverty. He made ends meet, by taking up tuition for school students.

It was a chance  meeting with V Ramaswamy Iyer in 1910, would be the turning point in Ramanujan’s life. Iyer was the founder of the Indian Mathematical Society, and thanks to him, Ramanujan began to be recognized in the math circles of Madras.  He however wanted a regular job to make ends meet, Iyer felt that a genius like him should not be wasted in clerical jobs. He sent letters to his friends in Madras, one of em was R.Ramachandra Rao, the district collector of Nellore.

I was struck by the extraordinary mathematical results contained in the notebooks. I had no mind to smother his genius by an appointment in the lowest rungs of the revenue department.

In Madras he got to meet the then Nellore district collector, R.Ramachandra Rao, who initially doubted that such a genius was original.  However with persistence from Rao’s friend, Rajagopalachari, he had a long discussion with Ramanujan over elliptic integrals and divergent series.  Rao, who was also the Secretary for the Indian Mathematical Society, was now convinced about Ramanujan, and supported him financially. With the help from Ramaswamy Aiyer, Ramanujan  managed to get his work published in Journal of the Indian Mathematical Society.

One of the first problems Ramanujan posted in the journel was to find the value of what is called the infinite nested radicals( pic1). After 6 months when none failed to answer it. he himself posted the solution, this equation was to solve infinitely nested radicals.

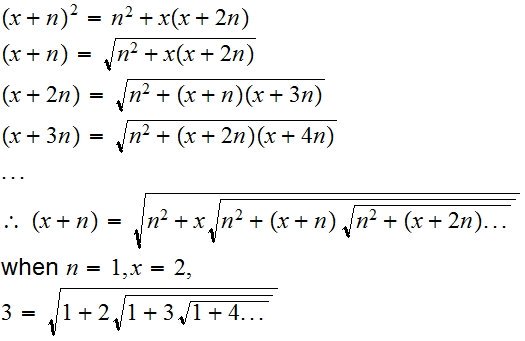
Ramanujan’s first formal paper for the Maths Journal was on Bernoulli Numbers and their properties. He came up with his own method of calculating Bn, based on previous Bernoulli numbers. The entire paper had 3 proofs, 2 corollaries and 3 conjectures. Basically Ramanujan’s method to calculate Bn was based on this 1) Bn is a fraction, and the numerator in it’s lowest wud be a prime number 2) Denominator of Bn contains each of factors 2, 3 only once 3) 2^n(2^n-1) Bn/ is an integer.

He however had a rather erratic style of writing, often not too clear enough,  and this  made his work quite hard to understand for the average reader. He had the most innovative methods to solve problems, yet his not too clear writing style and precision, could make it hard for others to understand.

Sir,
I understand there is a clerkship vacant in your office, and I beg to apply for the same. I have passed the Matriculation Examination and studied up to the F.A. but was prevented from pursuing my studies further owing to several untoward circumstances. I have, however, been devoting all my time to Mathematics and developing the subject. I can say I am quite confident I can do justice to my work if I am appointed to the post. I therefore beg to request that you will be good enough to confer the appointment on me.

The above application in 1912, along with a letter of recommendation from his Maths Professor, E.W.Middlemast at Presidency,  ensured he got a job as a clerk in the Accounts Department of the Madras Port Trust. During his spare time, he would still continue his research in mathematics. He was encouraged by his boss, Sir Francis Spring and his colleague, S.Narayana Iyer. Some of his friends like Spring, Narayana Iyer, Ramachandra Rao and Middlemast, helped him to send his work for Cambridge University, but he was rejected due to lack of formal educational qualifications.

In 1913 Middlemast, Narayana Iyer and Ramachandra Rao, presented Ramanujan’s work to British mathematicians. MJM Hill rejected him saying that though he was talented, he did not have a formal educational background, but he gave him valuable suggestions.  Encouraged by Hill’s suggestions, Ramanujan sent his works to Cambridge, two of them HF Baker, and EW Hobson did not show interest. On Jan 16, 1913, he wrote to G.H.Hardy and that would prove to be a turning point in his life. Hardy was amazed by Ramanujan’s take on the Bauer Theorem, what really impressed him was his next work on infinite series derived from a class called hypergeometric series. This class had earlier been researched by Euler and Gauss. By the time he finished reading Ramanujan’s work, Hardy was completely impressed, mind you he was one of the leading mathematicians of that time. He figured that his theorems must be true, because none wud really have the imagination to invent them.

Hardy requested Ramanujan to come to Cambridge, but he refused, due to the then prevailing sentiment of not going to a foreign land, strongly rooted in Indian society. For the time being, he was given a research grant at the University of Madras, where he did pioneering work on Frullani’s 1821 integral theorem. Hardy’s colleague Neville, again asked Ramanujan to come to Cambridge, and this time Ramanujan agreed. According to a popular anecdote, his mother had a dream, in which their family goddess Namagiri, commanded her not to stand in the way of her son’s progress.  From 1913-18, Ramanujan spent 5 fruitful years in Cambridge, collaborating with Hardy and Littlewood, on many research projects. While Littlewood said that “this man was at least a Carl Gustav Jacob”, Hardy remarked that he can be compared only with Euler or Jacobi.

In March 1916, Ramanujan was awarded the Doctorate for his research on highly composite numbers. Hardy later remarked that this was one of the most unusual papers he had ever seen. Both of them had contrasting ways of working, Hardy followed the Western model of proof and rigor, and was an atheist. Ramanujan was a devout believer and often relied on intuition and gut feeling. It was the perfect mix of East and West. On Oct 1918, he became the first Indian to be elected as Fellow of Trinity College, Cambridge. In 1917, he became a member of the London Mathematical Society. In 1918 he became the second Indian to gain fellowship of the Royal Society, and one of it’s youngest members. Sadly his poor health meant Ramanujan had to return back to India, and he passed away in Kumbakonam on this date in 1920, he was just 32, a beautiful mind, that left the world at a very young age. However his wife Janaki Ammal, took up the cause of her husband’s work. Though having no children, Janaki Ammal adopted Narayanan in 1950 who later became an officer with SBI. She ensured Ramanujan’s work was known to the public, many prominent mathematicians visited her when they came to India. She later passed away in 1994.

Work

Ramanujan came up with his own variant of the Brocard’s problem, which asks to find for integer values of n and m, where n!+1=m2. Still remains an unsolved problem, as only 3 integers, 4,5 and 7 have been found as solution for this.

Another is the Landau- Ramanujan constant, Landau here stated it first in the Limit form, later Ramanujan approximated N(x) as an integral. Basically it states that for large X, number of positive integers below are sum of 2 squares.

Ramanujan Theta Function generalizes the Jacobi theta functions, in a much more elegant manner. And this is used a lot in the Bosonic String Theory, M-Theory and Superstring theory.

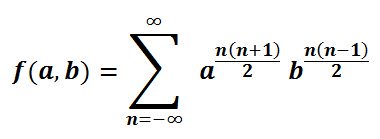
His home state of Tamil Nadu celebrates his birthday as State IT day, while Government Arts College, Kumbakonam remembers the day as Ramanujan Day.  It is fitting that his birthday should be declared as National Mathematics Day by Government, a truly great Indian.